Расчет сильфонных компенсаторов на прочность

Аннотация: Приведен метод и алгоритм численного анализа напряженно-деформированного состояния компенсаторов сильфонного типа.

Ключевые слова: Сильфонный компенсатор, малоцикловая прочность, метод конечных элементов.

Применение сильфонных элементов трубопроводов в различных отраслях промышленности достаточно распространенное. Применяя сильфонные элементы трубопровода, для компенсации температурных деформаций конструкций, повышаются рабочие параметры оборудования, структура производственных объектов упрощается, сокращаются габариты. Многолетняя эксплуатация сильфонных компенсаторов и применение их при строительстве трубопроводов являются наглядным примером превосходства сильфонных компенсаторов. Кроме того, применение сильфонных компенсаторов позволяет снизить потери тепловой энергии и затраты при строительстве и эксплуатации тепловых сетей. Результат применения сильфонных компенсаторов существенный с точки зрения технических и экономических показателей.

Как правило сильфонные компенсаторы подвергаются повторным воздействиям нагрузки с ограниченным числом циклов (102-104). Нагрузка определяется количеством пусков и остановок, изменений режимов оборудования за время работы. В условиях ограничения работы компенсатора область упругих изменений не позволяет полностью использовать его компенсирующую способность. Что бы увеличить ход сильфонного компенсатора следует допустить пластические деформации в наиболее нагруженных зонах оболочки. Так как циклическое упругопластическое деформирование сильфона сопровождается малоцикловым разрушением, возникает постановка задачи в обеспечении долговечности конструкции.

Возникают затруднения с разработкой строгих методов расчета сопротивления конструкций малоцикловому разрушению. Решение необходимых практических задач обусловили использование инженерных методов. Данные методы, основаны на сочетании результатов упругого расчета с экспериментальными данными. Подобный подход к инженерным расчетам малоцикловой прочности сильфонных компенсаторов и ряда конструкций, принят так же в нормах расчета [2]. В практике, реализуя методы инженерии расчетной оценки малоцикловой прочности сильфонных компенсаторов необходимо располагать достоверными и удобными в применении методами, а так же алгоритмами расчета состояния сильфонов.

Основным элементом сильфонного компенсатора (рис. 1) является сильфон, т.е. осесимметричная упругая оболочка, разделяющая среды и способная под действием давления, температуры, силы или момента силы совершать линейные, сдвиговые, угловые перемещения или преобразовывать давление в усилие. Сильфон, состоит из участков тороидальных оболочек положительной и отрицательной мерой искревления поверхности в окрестности какой-либо ее точки, т.е. гауссовой кривизны. Участки плавно сопряжены кольцевыми пластинками или участками конических оболочек.

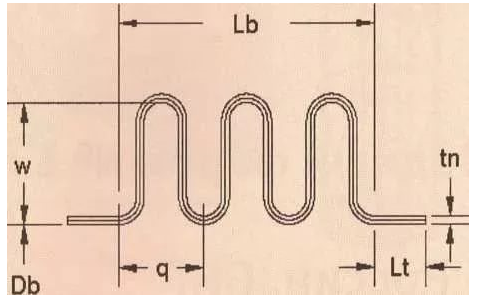
Рис. 1 — Расчетная схема сильфонного компенсатора

Патрубки, которые присоединяются к сильфону, представляют собой цилиндрические элементы толщиной h₁ и длиной Lt. Толщина стенки сильфона h. Характеристики материала (физико-механические) переменны вдоль меридиана оболочки и являются заданными функциями дуги меридиана s. Внутренним давлением q нагружен сильфон и нагрет до температуры Т. Задано относительное осевое перемещение торцов сильфонного компенсатора λ.

Для решения численным методом дифференциальных уравнений с частными производными, а также интегральных уравнений осесимметричной составной оболочечной конструкции, работающей в условиях осесимметричного термомеханического нагружения, используем оболочечный элемент (рис. 2). Оболочечный элемент ограничен двумя узлами i и j (i<j) Каждый имеет три степени свободы: осевое перемещение и, радиальное перемещение v, угол поворота нормали ϑ. Начало координат (s=0) помещается в узел i. Материал оболочечного элемента изотропный, упругий, подчиняется закону Гука. На данный элемент действуют нагрузка q_n распределенная по срединной поверхности элемента, нормальная к этой поверхности и распределенная по срединной поверхности элемента нагрузка q_τ, направленная по касательной к меридиану. Элемент может быть нагрет до температуры Т = Т₀ + ку (здесь у — расстояние от срединной поверхности элемента). Температура срединной поверхности изменяется вдоль меридиана по заданному закону T_o=T_o(s). По толщине стенки температура изменяется по линейному закону с заданным градиентом , где ∆T(s) — перепад температуры по толщине стенки.

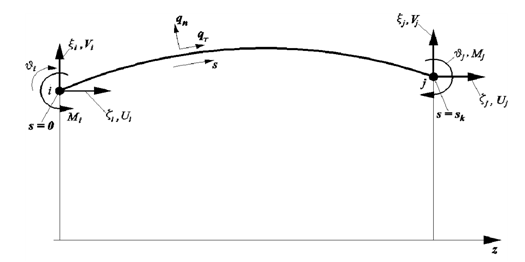
Вектора состояния,  где: U — осевое усилие в оболочке, V — радиальное усилие, М — меридиональный изгибающий момент, ζ — осевое перемещение точек координатной поверхности оболочки, ξ — радиальное перемещение точек координатной поверхности оболочки, ϑ — угол поворота нормали к срединной поверхности оболочки, r — радиус параллельного круга, T| - символ транспонирования.

Напряженно-деформированное состояние оболочечного элемента описывается системой линейных дифференциальных уравнений шестого порядка:

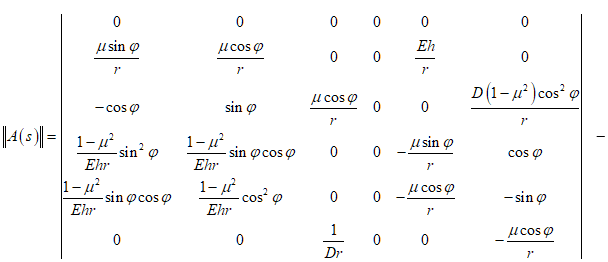 матрица коэффициентов системы,

Формирование разрешающей системы уравнений равновесия узлов системы:

,

где: [KG] — глобальная матрица жесткости всей системы, {δ} — вектор узловых перемещений; {R} — вектор внешних узловых усилий; {F_qT} — глобальный вектор узловых усилий всей системы, обусловленных силовым и температурным воздействием.

Формируем матрицу жесткости оболочечных элементов и шпангоутов для построения глобальной матрицы жесткости системы [KG]. Для построения вектора {F_qT} необходимо сформировать для каждого оболочечного элемента векторы краевых обобщенных усилий {V_qT}, обусловленные поверхностной нагрузкой и температурным воздействием.

В силу линейности системы (1) Установим зависимость однозначную между краевыми усилиями на торцах оболочечного элемента и краевыми перемещениями:

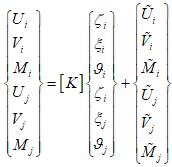
Здесь [К] — матрица жесткости оболочечного элемента размерностью 6*6, зависящая от геометрических и механических характеристик.

Столбцы матрицы жесткости [К] представляют собой обобщенные усилия на торцах элемента i и j,вызываемые единичными перемещениями этих торцов при отсутствии поверхностной нагрузки. Вектор {Ũ_i Ṽ̃_i M̃_i Ũ_j Ṽ̃_j M̃_j}^T является вектором краевых обобщенных усилий, обусловленных поверхностной нагрузкой и температурным воздействием на оболочечный элемент при нулевых смещениях торцов.

Расчет сильфонного компенсатора (алгоритм): формируем матрицы жесткости для оболочечных элементов системы. Решаем шесть однородных краевых задач для каждого элемента вида с граничными условиями, соответствующими единичным перемещениям торцов элемента:

Определяем векторы {V_qT} краевых обобщенных усилий для оболочечных элементов, выполняя для каждого элемента решение неоднородной краевой задачи (1) с нулевыми граничными условиями. Для решения систем дифференциальных уравнений (1), (2) применяем метод ортогональной прогонки. Формируем глобальную матрицу жесткости [KG] для составной оболочечной конструкции. Для формирования матрицы [KG] используем матрицы жесткости оболочечных элементов системы. Размерность матрицы жесткости [KG] равна 3 NU*3 NU, где NU — общее число узлов в системе. Формируем глобальный вектор узловых усилий {F_qT} из векторов {V_qT} краевых обобщенных усилий, построенных для оболочечных элементов системы. Размерность вектора {F_qT} равна 3*NU. По заданным внешним усилиям формируем вектор внешних узловых усилий {R} для всей системы. Размерность вектора {R} равна 3*NU. Отметим, что вектор {R} содержит не только заданные значения внешних силовых факторов, но и реакции наложенных связей (реакции опор). Выполняя операцию составления ансамбля [3], формируем разрешающую систему уравнений метода конечных элементов:

,

где {F}={R}+{F_qT} — глобальный вектор нагрузки; [KG] — матрица жесткости всей системы; {δ} — вектор узловых перемещений; {R} — вектор внешних узловых усилий; {F_qT}— глобальный вектор узловых усилий, обусловленных силовым и температурным воздействием на рассматриваемую конструкцию.

Преобразовываем матрицу жесткости системы [KG], а также глобальный вектор нагрузки {F} с учетом граничных условий. Если на узел п наложена связь с номером i, (i =1,2,3), то все элементы строки j = 3 (n-1) +I матрицы [KG] заменяем нулями, кроме диагонального элемента, который заменяем единицей. Элемент j = 3 (n-1) + i вектора узловой нагрузки {F} заменяем нулем. В результате получаем модифицированную матрицу жесткости [KG_мод] и модифицированный вектор нагрузки {F_мод}. Выполняем решение системы уравнений: . Находим все компоненты вектора узловых перемещений {δ}. Определяем реакции связей, наложенных на систему. Затем возвращаемся к не преобразованной матрице жесткости системы [KG]. Если на узел п наложена связь с номером i, (i =1,2,3), то формируем вектор {V}_j, из элементов строки j = 3 (n-1)+i этой матрицы. Размерность вектора {V}_j, равна 3*NU. Вычисляем произведение векторов Р = {V}_j{δ}. Реакцию связи вычисляем по формуле:

,

где {F_qT}_j —j — я компонента глобального вектора {F_qT} внешних воздействий на оболочечную конструкцию.

Расчет напряженно-деформированного состояния оболочечных элементов конструкции. Для каждого оболочечного элемента методом ортогональной прогонки выполняем решение краевой задачи для системы дифференциальных уравнений (1) с граничными условиями: ,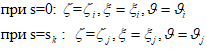

где: ζ_i, ξ_i, ϑ_i — перемещения i-го узла оболочечного элемента; ζ_j, ξ_j, ϑ_j — перемещения j-го узла оболочечного элемента. Все узловые перемещения определены на предыдущем этапе.

Таким образом, была определена задача при конечно — элементном анализе составной оболочечной конструкции в формировании разрушающей системы уравнений равновесия узлов. Предложена концепция метода и алгоритма численного анализа напряженно-деформированного состояния компенсаторов сильфонного типа.

Список литературы

1. Никольс, Р.В. Конструирование и технология изготовления сосудов давления. / Р.В. Никольс. Пер. с англ. — М.: Машиностроение, 1975. — 464 с.
2. Нормы расчета на прочность элементов реакторов, парогенераторов, сосудов и трубопроводов атомных электростанций, опытных и исследовательских ядерных реакторов и установок. — М.: Металлургия, 1973. — 406 с.
3. Зенкевич, О.С. Метод конечных элементов в технике. / О.С. Зенкевич. — М.: Мир, 1975. — 544 с.
4. Луганцев, Л.Д. Инженерный метод расчетной оценки несущей способности сильфонных компенсаторов при малоцикловом нагружении. / Л.Д. Луганцев. — Проблемы прочности, 1979, № 4, с.48- 53.

Calculation of compensators on stability

S. A. Glebovich

Abstract: The method and algorithm for numerical analysis of the stress-strain state of bellows-type compensators is presented.

Keywords: Bellows compensator, low-cycle strength, finite element method.

Glebovich Stanislav Aleksandrovich, graduate student, stivgl@mail.ru, Russia, Tula, Tula state university.