Аннотация
В данной работе изложены методы контурного анализа для распознавания образов на примерах распознавания простых объектов. Описаны необходимый математический аппарат, теоретическая часть контурного анализа. Рассмотрены основные методы распознавания изображений, а также предварительные операции, предшествующие контурному анализу. Проанализированы алгоритмы контурного анализа, доказана их практическая эффективность - инвариантность к масштабу и углу поворота объекта на изображении. Проанализированные алгоритмы были практически реализованы – на примере распознавания плоских геометрических фигур.
Введение
Контуры являются областями высокой концентрации информации, слабо зависящей от цвета и яркости. При рассмотрении какого-либо объекта в сознании человека формируется зрительный образ. При восприятии глаз отслеживает линию контура, что приводит к созданию в сознании образа с характерными деталями. Существует мнение, что при восприятии в сознании человека формируются два образа: контура и внутренней части изображения.
Контурный анализ является совокупностью методов выделения, описания и преобразования контуров изображений и распознавания зрительных образов.
Объект на изображении – плоская геометрическая фигура. Модель объекта – многомерный вектор, координаты которого характеризуют признаки объекта.
Целью данной работы является – распознавание изображений плоских объектов разных масштабов и ориентации в пространстве.
Классификация методов распознавания образов
1. Детерминированные – для построения алгоритмов распознавания используются геометрические меры «близости», основанные на измерении расстояний между распознаваемым объектом и эталонами классов.
2. Вероятностные – применяются вероятностные методы распознавания, основанные на теории статистических решений.
3. Логические – дискретный анализ и основанное на нем исчисление высказываний.
4. Структурные – для построения алгоритмов классов используются специальные грамматики.
5. Комбинированные – используется метод вычисления оценок.
Основная часть
Контурный анализ относится к детерминированным методам распознавания образов и имеет существенный недостаток – необходимо обеспечить отсутствие шума, кроме может быть «белого» на изображении путем предварительной обработки.
В нашем частном случае мы будем искать нормированное скалярное произведения между распознаваемым объектом и эталонным объектом в базе данных.
Собственно, для выделения границы изображения воспользуемся известным алгоритмом Канни, состоящем из пяти шагов:
· Сглаживание – размытие изображения для удаления шума (например, фильтром Гаусса).
· Поиск градиентов - границы отмечаются там, где градиент изображения приобретает максимальное значение.
· Утончение (подавление не-максимумов) - только локальные максимумы отмечаются как границы.
· Двойная пороговая фильтрация - применение порога, чтобы определить находится или нет граница в данной точке изображения.
· Трассировка области неоднозначности - упрощённо, задача сводится к выделению групп пикселей, получивших на предыдущем этапе промежуточное значение, и отнесению их к границе (если они соединены с одной из установленных границ) или их подавлению (в противном случае).
Далее стоит упомянуть способ кодирования контуров. В контурном анализе используется именно комплекснозначное кодирование, потому что операция скалярного произведения для векторов и для комплексных чисел - различны. Операции над контуром именно как над вектором комплексных чисел обладает необходимыми математическими свойствами, по сравнению с другими способами кодирования. Именно это обстоятельство и дает преимущество методам КА.
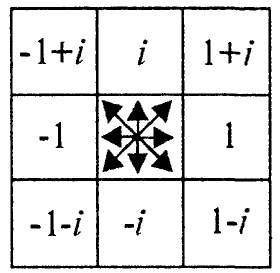
Рис 1. Координаты элементарного вектора при комплексозначном кодировании.
Контур объекта представлен совокупностью элементарных векторов. Элементарный вектор (далее ЭВ) γ(n) – вектор, соединяющий центры или узлы соседних контурных ячеек сетчатки, проведенный в направлении обхода.
Свойства комплесозначных кодов:
1) Коды 
инвариантны к переносу изображений.
2) При смещении на d элементов начальной точки 
происходит сдвиг номера ЭВ на величину d, т.е. 
В контурном анализе оперируют комплексозначным представлением контура в комплексном пространстве 
. Скалярное произведение в действительном координатном пространстве 
позволяет ввести не только норму для вектора этого пространства, но и обобщить понятие угла между векторами: 
. В пространстве НСП в общем случае является комплексной величиной и не может быть косинусом какого-либо действительного угла.
Существует такое понятие, как экстремальное свойство нормированного скалярного произведения (далее НСП) в . В соответствии с неравенством Коши-Буняковского для комплексных чисел имеем 
. На основании этого:
1) Модуль НСП в пространстве 
равен нулю, если контуры Г и N ортогональны, и принимает максимальное значение, равное единице, если Г и N – это один и тот же контур, причем контур N может быть повернут относительно контура Г на произвольный угол 
и изменен в масштабе в 
Простым языком НСП в может принимать значение 1, что означает высокую степень близости распознаваемого объекта эталонному.
2) Максимальное значение модуля НСП в инвариантно к преобразованию поворота ВК, т.е. если 
то модуль НСП сохраняет свое экстремальное значение независимо от угла поворота 
При этом НСП в таким свойством не обладает.
3) Значение максимума модуля НСП инвариантно к изменению масштаба контура за счет растяжения каждого его ЭВ в 
раз.
Инвариантность максимума модуля НСП в к углу поворота контура позволяет считать повернутые относительно друг друга контуры одними и теми же.
Результаты моделирования и их анализ
Как мы уже выяснили, признаком сравнения между изображением, приходящим на вход системы технического зрения и эталонного изображения, хранящегося в базе данных, является модуль нормированного скалярного произведения. Так же в программе присутствуют некоторые вспомогательные операции, предшествующие контурному анализу.
Эксперимент 1. Сравнение двух прямоугольников. Подаваемый на вход, в отличие от эталонного, повернут на 90 градусов.
Рис.2. Эталонное изображение объекта
Заранее известны координаты контура N эталонного изображения: N = 
Рис 3. Изображение, поданное на вход системы технического зрения (контур Г)
Опустим процесс бинаризации, применение алгоритма Канни для выделения границы второго изображения, соединение получившихся отрезков элементарными векторами и сразу же запишем координаты контура Г, пришедшего на вход системы технического зрения: 
. Квадраты норм контуров равны 
Скалярное произведение: 
.
Модуль НСП этих контуров в пространстве , равный 
свидетельствует о том, что эти формы абсолютно одинаковы.
Заключение
Основные выводы:
- Методы контурного анализа являются оптимальными для определения близости двух объектов, несмотря на имеющиеся недостатки.
- Методы контурного анализа требуют проведения предварительной обработки изображения.
- Контуры объекта, в отличии от его остальных точек, устойчивы на изображениях, полученных в разное время, разных ракурсах, условиях погоды и при смене датчика.
- Контуры позволяют создать простые аналитические описания изображений объектов, инвариантных к переносу, повороту и масштабированию изображения.
- Пространством, в котором целесообразно проводить контурный анализ, является 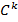. Элементарные векторы контура адекватно отражаются в нем комплексными числами.
- Показано, что модуль нормированного скалярного произведения двух контуров, рассматриваемых, как векторы, является характеристикой близости этих контуров, инвариантной к преобразованиям переноса, поворота и масштабирования.
Список литературы
- Фурман Я.А. Введение в контурный анализ/ Я.А. Фурман, А.В. Кревецкий, А.К. Передреев. —
2-е изд., испр. — М.: ФИЗМАТЛИТ, 2003. — 592 стр. - Леухин А.Н. Многомерный гиперкомплексный контурный анализ и его приложения к обработке изображений и сигналов/ А.Н. Леухин — М.: МарГТУ, 2004. — 36 стр.
- Гонсалес Р. «Цифровая обработка изображений»/ Р. Гонсалес, Р. Вудс,
2-е изд.испр.- М.: ТЕХНОСФЕРА, 2012 — 1104 стр. - Warkenar C.S. A heuristic clustering algorithm using union of overlapping pattern-cells/ C.S. Warkenar, G. Krishna, M.: Pattern recognition, 2000. — 85 стр.